こんにちは。KEC茨木本校2230です。
12月に入り,秋入試もいよいよ終盤ですね。
今回は,12/2実施の近畿大公募,理系数学第2問を解説します。
数Ⅱの積分,放物線2つに円が絡んだ図形の面積を問う問題でした。
(1) 点Pのy座標,点Qのy座標
それぞれ連立して解くだけです。y座標を聞かれているので,不要なxを消去しましょう。結果,Pのy座標は√2,Qのy座標は1になります。
(2) 線分OPと曲線y=f(x)で囲まれた図形の面積
Pの座標は(√2,√2),線分OPの方程式はy=xです。
求める面積は定積分で次のように表せます。
\({\int_{0}^{\sqrt{2}}(x-f(x))dx}={\int_{0}^{\sqrt{2}}(x-\frac{\sqrt{2}}{2}x^2 )dx}\)
これを計算すると1/3となります。
なおここは,放物線と直線で囲む図形の面積の奥義「1/6公式」がハマりますね。
これを用いれば,線分OPの方程式はもちろんのこと,定積分の計算作業もハショレて,
\(\frac{1}{6}・\frac{\sqrt{2}}{2}・(\sqrt{2})^3=\frac{1}{3}\)と求められます。
(3) 曲線Cと線分OQと線分ORで囲まれた図形の面積
Qの座標は(√3,1),∠QORの大きさはπ/6です。
求めるものは,半径2で中心角π/6の扇形OQRの面積で,\(\frac{1}{2}・2^2・\frac{π}{6}=\frac{π}{3}\)です。
(4) 曲線Cと線分ORと曲線y=g(x)で囲まれた図形の面積
まず,線分OQと曲線で囲まれた図形の面積を,(1)と同様に求めます。
定積分では,\({\int_{0}^{\sqrt{3}}(\frac{1}{\sqrt{3}}x-g(x))dx}={\int_{0}^{\sqrt{3}}(\frac{1}{\sqrt{3}}x-\frac{1}{3}x^2)dx}\) ですが,ここもあの公式で\(\frac{1}{6}・\frac{1}{3}・(\sqrt{3})^3=\frac{\sqrt{3}}{6}\)となります。
次に,求めるべき面積ですが,これは(3)の扇形から今求めたものを引くことで,\(\frac{1}{3}-\frac{\sqrt{3}}{6}\)となります。
(5) △OPQの面積
これ,案外クセモノでしたね。
最速は \(\frac{1}{2}\left|\sqrt{2}・1-\sqrt{3}・\sqrt{2}
\right|=\frac{\sqrt{6}-\sqrt{2}}{2}\) です。2点P,Qのx,y座標をテレコにかけて引くヤツ。
むしろ真っ先にやりたくなるのは,\(\frac{1}{2}\)・OP・OQ・sin∠POQ ですが,
∠POQがπ/12なので困るかも。そこで,,,
三角形をぶった切りましょう。Qから真横に補助線を引きます。
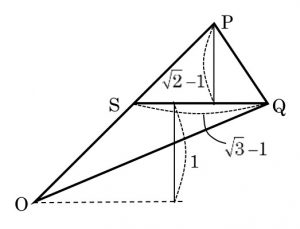
OPと交わる点Sの座標は(1,1)になります。SQを底辺とする2つの三角形,△PSQと△SOQに分かれましたね。高さはそれぞれ√2−1と1,足し合わせると√2,よって△OPQの面積は \(\frac{1}{2}・(\sqrt{3}-1)・\sqrt{2}=\frac{\sqrt{6}-\sqrt{2}}{2}\) となります。
(6) 曲線Cと曲線y=f(x)と曲線y=g(x)で囲まれた図形の面積
(2)と(4)で考えた図形をうまく使いましょう。
扇形OPRから(2)と(4)の図形を取り除けば,注目している図形になります。
扇形OPRは半径2で中心角なので,この面積は \(\frac{1}{2}・2^2・\frac{π}{4}=\frac{π}{2}\)です。よって,求める面積は \(\frac{π}{2}-\frac{1}{3}-(\frac{π}{3}-\frac{\sqrt{3}}{6})=\frac{π}{6}+\frac{\sqrt{3}}{6}-\frac{1}{3}\) です。
(1)ではx座標でなくなぜy座標を求めさせたのか。(5)は必要か。など気になるところはありますが,(6)まで順次お膳立てしてくれている問題でした。奇抜なこともなく素直に取り組やすい良問と思いますが,受験生の皆さんはいかがだったでしょうか。

