こんにちは。KEC茨木本校2230です。
多くの高校生にとって,まもなく定期試験ですね。
高1生にとっては2回目で,前回の反省から取り組みを改善なさったことでしょう。
そんなわけで,2230も質問対応におわれております。
数学はもちろん,化学や物理も来たれ。

今週も,平日土日と時間の空く限り対応します,どしどしいらしてください。
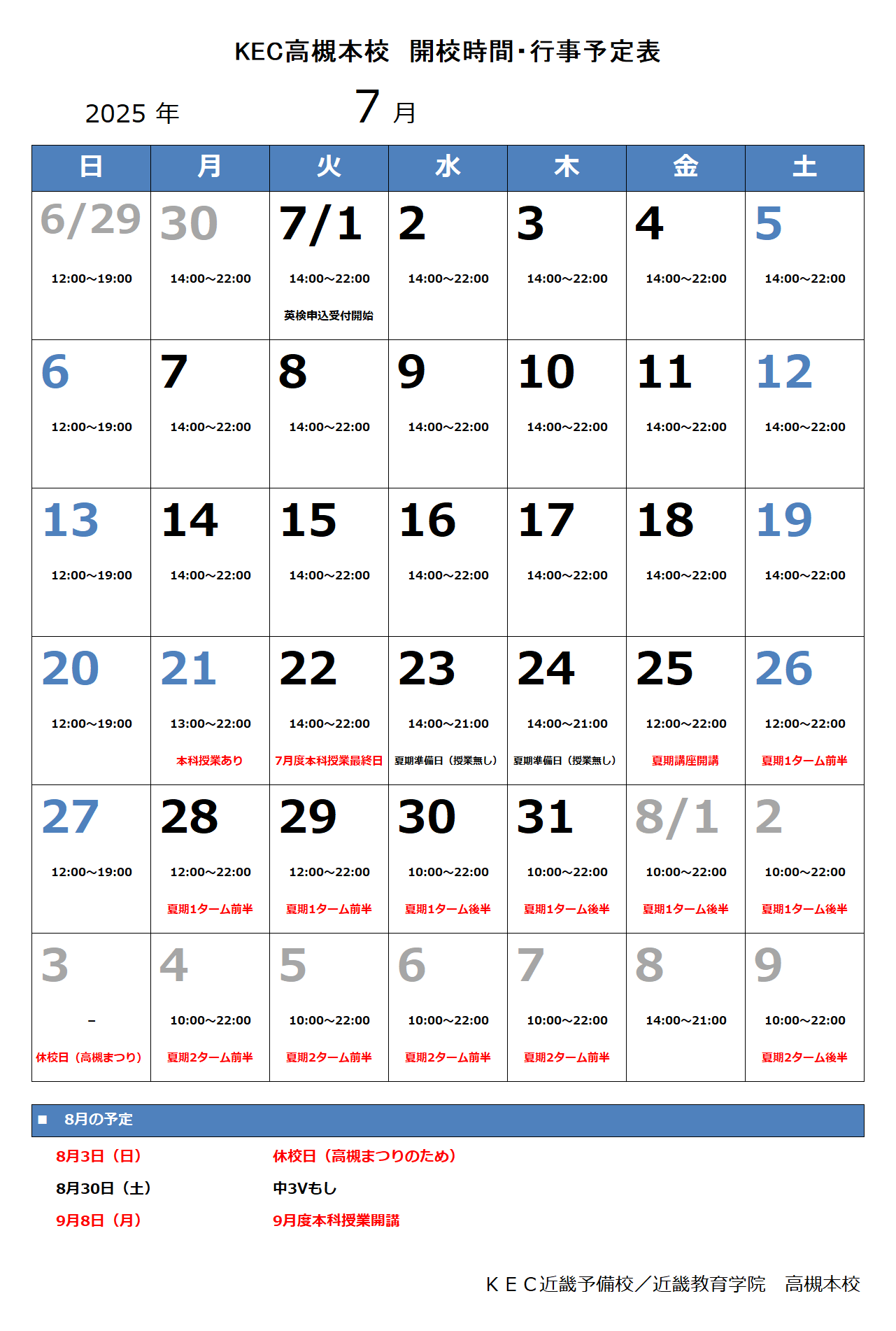
2025年7月度の予定表【高槻本校】
先日、学生アシスタントとの会話で発覚(?)したのですが、三島高校の昨年と一昨年のトップ(教育長賞)の生徒が高槻本校の卒業生だったそうです。
2人とも自分から言うタイプではなかったので、最近まで知りませんでした。
メンサに入会したことを授業で言いふらしている川渕とは違い、慎み深い卒業生達で、さすがですね。
さて、2025年7月度の高槻本校の予定表は以下の通りです。
いよいよ夏期集中講座が始まります。
夏期講座期間は、8月3日(日)のみ休校で、他の日はお盆期間も含め開校しています。
夏期中は、KEC卒業生の学生アシスタントも早い時間から勤務していますので、わからないことがあったら遠慮なく質問してください。
PDF版はこちら→2025年7月度開校予定表_高槻本校
*********************************
■合格体験談・総集編はこちら
■KEC高槻本校公式サイトはこちら
■各種イベントのお申し込みはこちら
■アシスタントブログの総集編はこちら
■動画をふくむブログの総集編はこちら
■プリントをふくむブログの総集編はこちら
勉強の息抜き
こんにちは!枚方本校アシスタントの山口です!
大雨の日や蒸し暑い日が続き、過ごしにくい日々で疲れることが増えるので、
体調管理には気をつけましょう!
皆さん、お勉強の調子はいかがでしょうか?
私は今週、臨床病態学、小児看護学概論という科目で中間テストがあったのですが、
手応えがあまりなく落ち込んでいます…。
もうすぐ皆さんも期末テストが来ると思いますが、あまり気負わずに適度に
息抜きをしながら、一緒に頑張りましょう!
今回は私がおすすめする勉強の息抜きの方法を紹介します!
それは、散歩です!
勉強の合間の散歩は気分転換やリフレッシュに効果的です!
散歩をすることで脳の血流がよくなり集中力や思考力が向上し、日光を浴びると
リラックス効果があるセロトニンが分泌され、いいこと尽くしです!
ですが、最近、夏と思えるほどの猛暑が続いているので、
熱中症には注意しましょう!
自分のペースを守って勉強に打ち込みましょう!
******お問合せ先******
“宇宙一キミと向き合う塾予備校”
KEC近畿予備校・KEC近畿教育学院 枚方本校
https://www.prep.kec.ne.jp/
TEL:072-845-7700
*****************
中学生の大活躍!
みなさんこんにちは。小学生、中学生、高校生みんなの塾予備校、高槻芝生校の小林です。
さて今日は中学生さんの定期考査の結果をお伝えです(中1生さんはまだ結果が出ていないので取り敢えず途中報告)。
中2生さん 487点!
中3生さん 481点!
二人とも天才だから楽々この点数を取っているんじゃない。
コツコツコツコツ頑張ってこの点数を取っています。
地道な努力って実はとても大変です。なんせ派手さはありませんし、基礎基本を押さえることって地味なので、ついつい派手な応用に行きがち。けど、実はそれではいけない。きっちりと基礎を固めないと。そこをこの二人は怠らない。だからこの点数です。
基礎基本をきっちりと勉強してもらう風土が高槻芝生校にはあります。それを可能にするベテランしかいない。一度体験に来て頂きたいと思います。
☎072-694-8822
(受付時間=14時~21時)
大学入試2025年度・逆転合格速報【KEC近畿予備校】
皆さん、こんにちは。
もうすぐ7月。受験生に取って、勝負の夏がやってきます。
皆さん、がんばってますか???
新学年のスタートが落ち着き、この時期に2025年度大学入試の振り返りと検証を行っています。
その振り返りと検証の際に、模試の結果と進学先の相関関係を調べています。
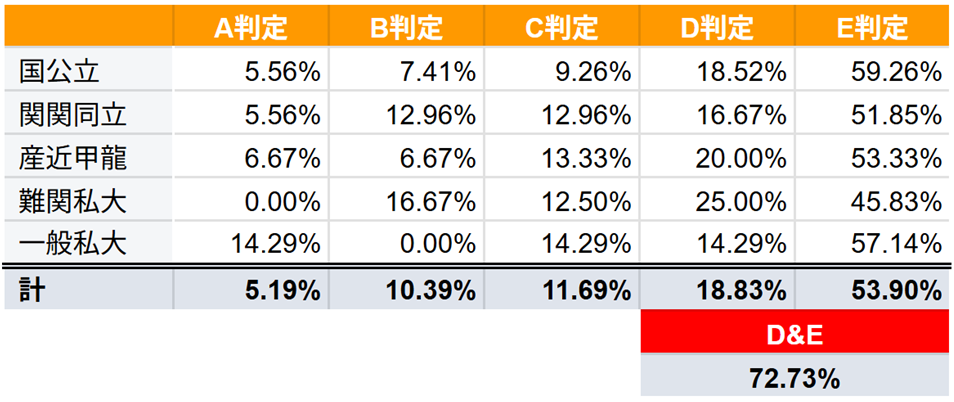
下の表は、2025年度4月に大学に進学したKEC近畿予備校生の第1回全統共通テスト模試(2024年5月実施)の合否判定別の比率です。
ご覧のように、A~C判定だった生徒が27.27%、D判定&E判定からの逆転合格を果たした生徒が72.73%となっています。
恐らく、今の時期、様々な模試の結果が返って来ています。
D判定&E判定だった方、現段階で志望校変更等をしないことをお勧めします。
しかしながら、楽観的にはならないでください。
この昨年のD判定&E判定だった方々は、間違いなく、ここから相当がんばっています。
判定に寄りませんが、
模試のあとはしっかりと解き直しを行い、
結果が返って来た際には、苦手分野の確認とその対策を行ってください。
特にD判定&E判定だった方は、今、行っている学習法に問題がある可能性があります。
KEC近畿予備校に通われている方はKECの専任講師に、
そうでない方は通われている塾予備校の先生や学校の先生に、
何をすべきかを相談するようにしてください。
夏の後だと取り返しがつかない場合が多いので、正に今の時期に、相談を行ってください。
KECにはD判定&E判定からの逆転合格のエビデンスがあります!
現状がどうあれ、皆さんの志望校合格を信じて、指導&アドバイスを行います。
皆さん、がんばりましょう!
■■■■■■■■■■■■■■■■■■■
KEC夏期集中講座・受講生募集中!

夏期集中講座の詳細は、
https://www.prep.kec.ne.jp/summer/
をご覧いただくか、
〔総合TEL〕0120-99-1919
までお電話ください。
■■■■■■■■■■■■■■■■■■■
息抜きにおすすめのスポット3選!
こんにちは!KEC枚方本校アシスタントの岡です。
去ったと思った梅雨前線が舞い戻り、天気の悪い日が続いていますね。湿度も気温も高く、過ごしにい時期ではありますが、服装などを工夫して乗り切りましょう!
さて、今回は枚方本校周辺のおすすめ息抜きスポットを3つ紹介します!
1つ目は枚方モールのマクドナルドです!ここの魅力は何と言ってもその近さにあります。アルタイル館から徒歩1分、ポテトをアツアツのまま持ち帰り、塾の休憩スペースで楽しむことだって余裕です。
2つ目はT-SITE内のスターバックスです!自習疲れに糖分を取りたくなったら、ここでフラペチーノを注文しましょう。眠気覚ましの散歩がてら、コーヒーを買いに行くのもおすすめです。
3つ目はT-SITE地下のLIFEです!勉強の息抜きにスーパー?と思う方もいるかもしれませんが、侮るなかれ。LIFEはスーパーなだけあって品揃えが多く、飲み物やカップ麺お菓子にアイスも、コンビニよりよっぽど安く買えます。自分が受験生だったころは、気分転換も兼ねてよくLIFE内を散策していました。
今回は枚方本校周辺のおすすめ息抜きスポットを3つ紹介しました。皆さんもこうした場所を有効活用し、勉強のために活力を養いましょう!
*******************
“宇宙一、キミと向き合う塾・予備校”
KEC近畿予備校・KEC近畿教育学院
<公式HP>
KEC近畿予備校・KEC近畿教育学院 公式ホームページ
<お問合せ電話番号>
[フリーダイヤル] 0120-99-1919
*******************
アシスタントブログ 第18弾! 【高槻本校】
初めまして!KEC高槻本校アシスタント新1回生の本田です。
今回は初めてブログを書くので、私の通っている「大阪公立大学」について紹介します!

大阪公立大学は2022年4月に「大阪市立大学」と「大阪府立大学」が統合してできた比較的新しい大学です。
学部は、現代システム科学域とかいうかっこいい名前の学域をはじめ、商学部や工学部など1学域11学部で構成されています。ちなみに私は看護学部に入学しました!学生数も1万2000人を超え、北海道や九州からも学生が来ているので、キャンパス内では様々な方言が飛び交っています(笑)
大阪公立大学には6つのキャンパスがあります!私は3キャンパスを経験する激レアな年度に入学したのでそれぞれの魅力を紹介します。
まずは、1回生の前期に利用する中百舌鳥キャンパスです。このキャンパスは自然が豊富で、最近の暑さでアゲハ蝶とセミが共存する異常現象が起きています。次に、森ノ宮キャンパスです。今年の9月に大阪城ホールの近くに新しく開設される予定なので、とても楽しみにしています。キャンパスがきれいだとモチベーションが上がるので本当におすすめです。しかし私は看護学部なので森ノ宮キャンパスにお世話になるのは1回生の後期だけらしいです。残念です…。2回生からは医学部の人と一緒に仲良く天王寺にある阿倍野キャンパスで学びます。あべのハルカスの横にあるキャンパスなので、おしゃれなお店にたくさん行きたいです!もちろん、駅周辺には安い・早い・旨いのお店もたくさんあるのでみんなでワイワイ楽しむ予定です。
施設以外のおすすめポイントとしては、毎回の授業でキャンディをくれる韓国語の先生やアイマスクをくれる教授など、学生の眠気を吹き飛ばそうと全力になっている先生方がいることです。さらに、KECの先生方に負けないぐらい笑いに貪欲な教授が沢山います!ぜひ、入学して自分の目で確かめてみてください!
今回を通して、少しでも大阪公立大学に興味を持ってくれたら嬉しいです!
ではまたどこかで会いましょう!
*********************************
■合格体験談・総集編はこちら
■KEC高槻本校公式サイトはこちら
■各種イベントのお申し込みはこちら
■アシスタントブログの総集編はこちら
■動画をふくむブログの総集編はこちら
■プリントをふくむブログの総集編はこちら
で,行ってきました。
こんにちは。KEC茨木本校2230です。
先週,いばきたエリアを紹介しましたが,早速行ってきました。
梅雨の中休み,晴れ間広がる土曜の午前,もちろんチャリです。

府道46号,長ヶ橋分岐を桑原橋方面へ,ふれあい運動公園からの遠景。
46号高架橋の股下からダムが,そして吊橋の一部が見えます。

大門寺トンネルを過ぎてしばらく,ダムパークいばきた到着。車も多く来てます。

いざ,グラビテート大阪。
6月は茨木市民と市内在勤者の入園料は0円ですが,吊橋通行はふつうに1,100円です。

いやぁ,アンカレッジ萌え。力強く美しいっす。

茨木童子がお出迎えなのですね。
ケーブル揺れてます,橋も揺れてます。
歩みだすと左右に揺れて酔っぱらい状態に。それでも直に慣れます。
足元を見るとこんな感じです。


まっすぐ,気持ちいいいです。
ダムのこっち側が見えます。

橋とダムのセットです。

日本最長420mを堪能,なかなかの迫力でした。

ダムカードとマンホールカード,ゲット!
2230はチャリでしたが,一般の方々はバスがいいかも。いばきた,よかったらどうぞ。
眠気に勝とう!
皆さんこんにちは!枚方本校アシスタントの北條です。
最近気温が高くなってきているので、熱中症に気を付けましょう!
勉強をしている時の眠気覚ましに、エナジードリンクを飲むこともあると思います。しかしエナジードリンクを飲んだのに糖分によって逆に眠たくなってしまったという経験をした人も多いのではないでしょうか。そんなときに、糖分の少ない飲みやすい飲料を紹介します!
伊藤園の『お~いお茶 濃い茶 PREMIUM STRONG PET 470ml』です。
この商品は、他のエナジードリンクと変わらない量のカフェインが含まれている上に、糖質がほとんど入っていないのですが、普段のおーいお茶と変わらず、非常に飲みやすい緑茶になっているので、普段の水分補給にもオススメです。
カフェインを取って勉強をするのも良いと思いますが、普段からしっかり睡眠時間を確保して、健康的な受験生生活を送りましょう!
*******************
“宇宙一、キミと向き合う塾・予備校”
KEC近畿予備校・KEC近畿教育学院
<公式HP>
KEC近畿予備校・KEC近畿教育学院 公式ホームページ
<お問合せ電話番号>
[フリーダイヤル] 0120-99-1919
*******************
新学部、新キャンパス
こんにちは!KEC枚方本校アシスタントの森本です。
6月も終わりに近づき、夏の暑さが本格的になり始めてきましたね。水分補給をこまめにして熱中症に気を付けましょう!
今回は僕の学部について紹介したいと思います。
僕は2025年度から開設された関西大学ビジネスデータサイエンス学部に通っています!この学部は、データサイエンスとビジネスを融合した学部で文系・理系どちらも進学することができます。また、カリキュラムも自分の学びたい分野について奥深く学べるよう選択肢が多くなっているのが魅力ですこれからの時代はAIの進化やデジタル化が加速しているため、「データを読み取る力」 「そこから価値を生み出す力」などの将来求められるスキルを身につけることができます。
この学部はキャンパスも新しく吹田みらいキャンパスがという場所です。また関西大学の本キャンパスである千里山キャンパスとの間に無料シャトルバスがあり、いつでも千里山キャンパスに遊びに行くことができます!開設されてまだすぐなので大学側もビジネスデータサイエンス学部の生徒が増えることも願っていました(笑)これからどんどん発展したキャンパスになると思うので、是非オープンキャンパスに来てみてください!
*******************
“宇宙一、キミと向き合う塾・予備校”
KEC近畿予備校・KEC近畿教育学院
<公式HP>
KEC近畿予備校・KEC近畿教育学院 公式ホームページ
<お問合せ電話番号>
[フリーダイヤル] 0120-99-1919
*******************