こんにちは。枚方本校アシスタントの神田です。
そろそろ夏休みですね。受験生のみなさんにとっては受験勉強の山場となる季節です。
模試を見据えながら、まわりを出し抜くつもりで勉強に本腰を入れていきましょう。

今回は数学Ⅱ、Ⅲに登場する定積分の話をしようと思います。
内容はタイトルの通りで、昔、私が躓いた疑問についての説明になります。
高校１、２年生の方はまだ習っていない範囲になってしまいますが、良ければ読んでいってください。

では積分の話に入ります。
皆さんが積分を習ったとき、最初に「微分の逆」の操作として不定積分を教わったと思います。積分定数Ｃを付け忘れることでおなじみですね。この次に、積分定数を考えなくていい方の積分として学習するのが定積分だったと思います。またこの際に、定積分は面積を求める計算だと学習したはずです。
ここからが本題です。みなさんは定積分の計算でなぜ面積が求まるのか、納得できていますか？
出来ていない、という方のために今回はこの理由について説明をしたいと思います。

積分と言えば微分の逆の操作の事を言いました。
であれば答えは簡単です。関数を積分した結果が面積になる理由は、その面積を微分した結果が積分する前の関数になるからです。
おそらく高校の数学の授業ではグラフとx軸の間の領域を縦長の長方形に分割して説明を受けたと思います。このブログでも同じ図解を用います。

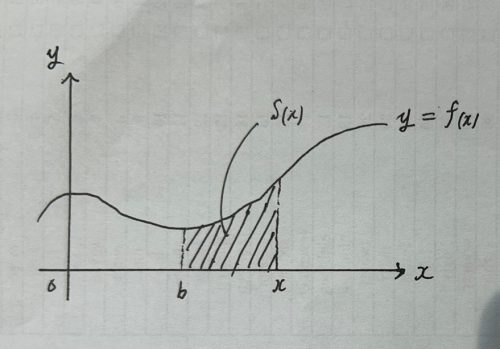
上のように適当なグラフｙ＝f(ｘ)と、x軸と、縦に伸びる２本の直線で囲まれる部分の領域を考えます。左端のx座標をb,右端のx座標をxとします。すると領域の面積はｘによって変化するのでS(ｘ)のように書けます。（ｂは一定として考えます）このS(ｘ)の微分がf(x)になることを調べます。(f(x)>0としました)

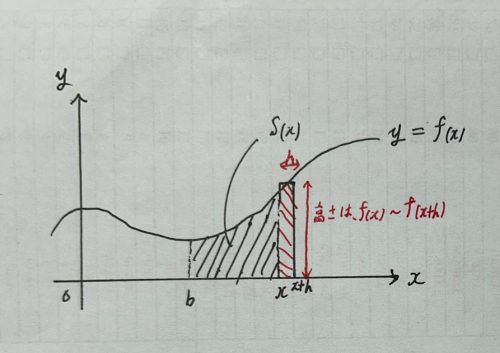
では次に先程の領域を右端のx座標を長さhだけ右にずらした時の面積はS(x+h)と書けて、微分はｘの瞬間的な増加に対する関数の変化量のことでしたから、

S'(x)≒{S(x+h)-S(x)}/h  (h→0で≒は=になります)

のようにかけるはずです。
この式の右辺の分母S(x+h)-S(x)は,x~x+hまでの領域の面積なので、横幅がh,高さがf(x)~f(x+h)の長方形の面積とほとんど等しくなります。（hが0に近づくほど等しくなります）
よって

S(x+h)-S(x)≒h×f(x)だから、
S'(x)≒{S(x+h)-S(x)}/h
　　≒f(x)×h/h
　　=f(x)
実際にはもう少し厳密に書けますが、とにかく面積の微分がグラフの関数になりました。
厳密にはf(x)×h＜S(x+h)-S(x)＜f(x+h)×hとしてh→0の極限を取ります。
このように、面積を微分すればグラフの関数になることがわかったので、積分は面積を求める計算になるとわかるんですね。

枚方本校には理系のアシスタントがたくさんいますので、こうした素朴な疑問があるときは先生がいなくても、遠慮せずにどんどん質問に来てくださいね。数学も物理も化学も大歓迎です。英語も人によっては答えられます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

“宇宙一、キミと向き合う塾・予備校”
KEC近畿予備校・KEC近畿教育学院

＜枚方本校公式HP＞
https://www.prep.kec.ne.jp

＜お問合せ電話番号＞
072-845-7700
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊