こんにちは。KECの塾・予備校部門，高槻本校の数学・理科担当の川渕です。
高校生のテスト期間が近づいてきました。
数学IIで最後に習う項目は微分・積分。
微分ではグラフの接線を求めたりしますが，今回は，その接線についてのお話です。

「接線を求めて何が嬉しいのかな・・・」と高校時代の私は思っていたのですが，大学生になってその活用法を知りました。
例えば「ニュートン法」というものがあります。
方程式の解を反復計算で求めるアルゴリズムです。
こんなイメージで計算していきます。

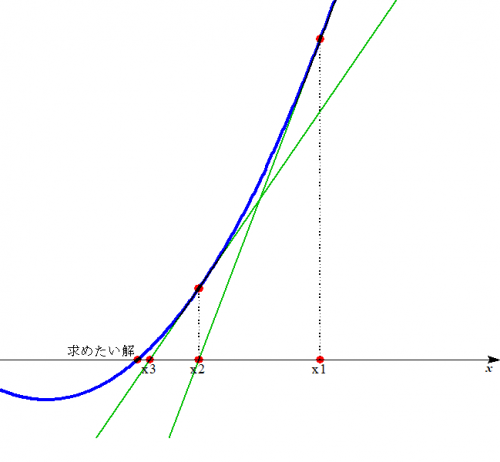
方程式をグラフにすると，x軸との交点が解を表します。
ここで適当なx＝x1でグラフの接線を引き，x軸との交点をx2とします。
つぎに，x＝x2でグラフの接線を引き，x軸との交点をx3として・・・
を繰り返していくと，求めたい解に近付いていきます。
これを利用すると，例えば，y＝x²－nのグラフから√nの近似値を求めることができます。
反復計算はコンピュータが得意とするところ。
そこで，恒例の（？）スクラッチでコードを書いてみました。

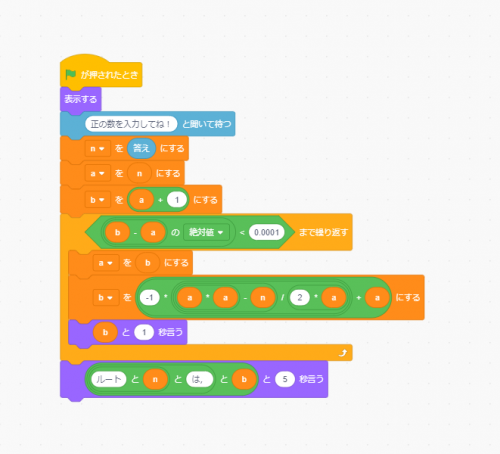
繰り返し部分にややこしそうな数式がありますが，これは，x=aにおけるy＝x²－nの接線とx軸との交点を計算する式です。
これが漸化式になっていて，求まった値を次々代入することで√nに近づいていきます。
実行すると，こんな感じになります。
　

　
高校数学は，後半になるにつれ応用例が増えてきます。
大学で理工系に進むと、たいてい微分・積分が必修です。
KEC高槻本校では，冬期講習から始まる「リスタート数学」で数II，数Bの復習をし，2月から数IIIを開講します。
この機会に数学の反復学習をしたい方は，ぜひ，KEC高槻本校にお問い合わせください。

■合格体験談・総集編はこちら

■KEC高槻本校公式サイトはこちら