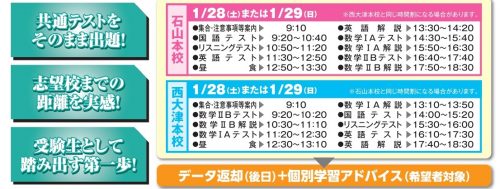
こんにちは。KEC茨木本校2230です。
受験生が国公立大2次試験や公立高対策の最中,2230は願掛けと観梅に出かけました。
長岡天満宮(長岡京市)と上宮天満宮(高槻市)です。
まずは長岡天満宮。最寄り駅は阪急長岡天神かJRなら長岡京,昔の神足ですね。
でも2230はチャリで西国街道60分です。

圧巻の酒樽たちがお出迎えしてくれます。
境内はこちらです。

手前には仔牛。実物はかわいいです。後で出てくるのとどちらがお好みでしょうか。

紅梅が咲きつつあります。

絵馬もいい感じ。

「ど冷えもん」なる自販機発見。なんか書いてある。
ポンポン山のたぬきさん
他を抜き合格どらやき
そら買わない手はない。

次は上宮天満宮。JR高槻,北側バスロータリーからまっすぐ参道。
2/25,26は4年ぶりの天神まつり開催とのこと,出店も多く賑わっています。

お参りの皆さんで大行列,正月のようです。

こちらにもかわいいのがいますよ。

絵馬も様々に。

梅は7分咲きってところでしょうか。

ローアングルから水仙と梅。

春はもうすぐ。願掛けして吉報を待ちます。