こんにちは。KECの塾・予備校部門,高槻本校の数学・理科担当の川渕です。
高槻本校は,8月14日(土)~17日(火)の4日間,お休みを頂いています。
8月18日(水)から,夏期講習の第3タームを開講します。
夏期講習の前半期間,小学生の塾生から,こんなことを言われました。
「先生,サイン・コサインって,いつ使うん?」
サイン・コサインを習うのは高校の数IA。
小学生がそれを知っているのは優秀ですが,しかし,この発言には,「サイン・コサインを習って何の役に立つの・・・」といったニュアンスも含まれる気がします。
サイン・コサインは,もちろん,とても重要な関数です。
一例を挙げると,大学の専攻によっては数学で「フーリエ級数」を習います。
ざっくりいうと,いろんな関数を三角関数の和で表す技です。
例えば,こんな関数も近似できます。
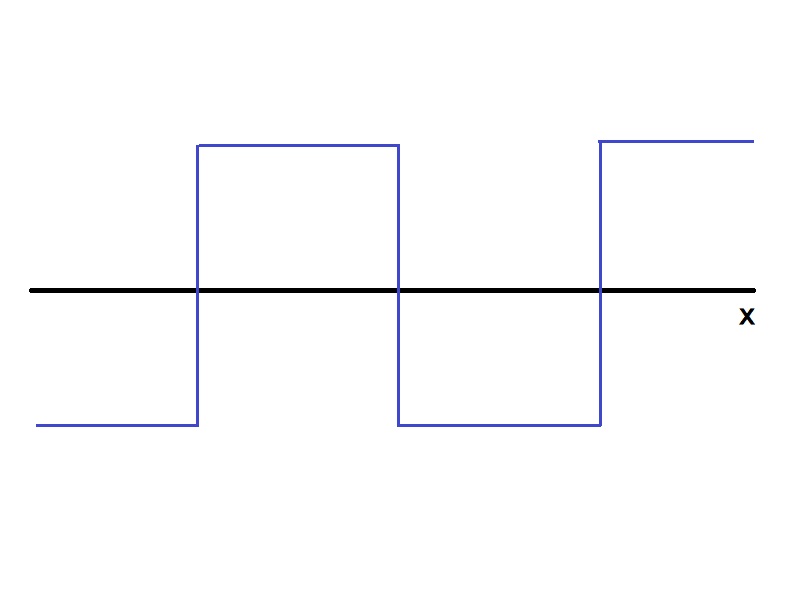
上記の形のグラフは,細かい議論は抜きにして,
sin x + (sin3x)/3 + (sin5x)/5 + ・・・ + {sin(2n-1)x}/(2n-1) + ・・・
という無限級数の和を利用することで近似できます。
実際に,sin x,sin x +(sin3x)/3,sin x + (sin3x)/3 + (sin5x)/5,と少しずつ項を増やしてグラフを描くと,だんだん目的の関数に近付くようすがわかります。
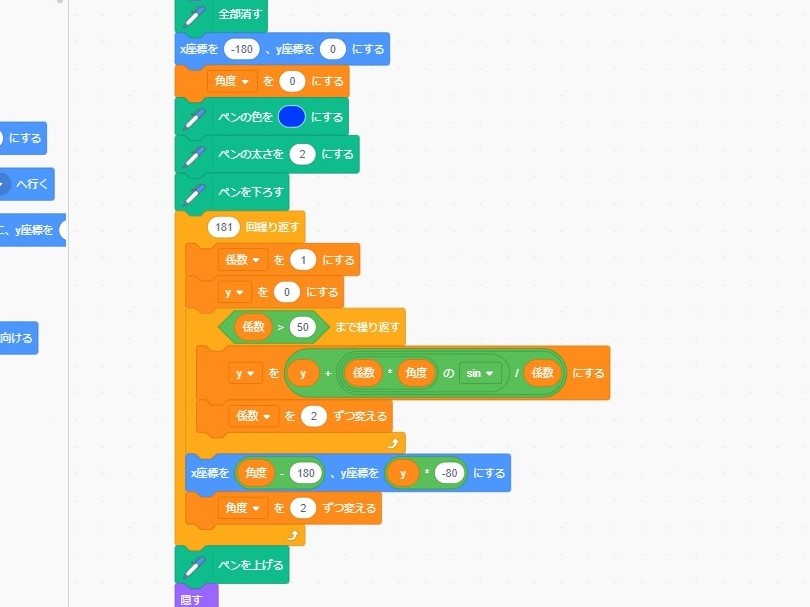
ということで,恒例のScratchで表現してみました。
n=1,n=2,n=3,n=4,n=10,n=50の場合を順に描いています。
手計算でこんなことをするのは大変ですが,さすがコンピュータ。
難なくこなします。
Scratchは子ども向けのプログラミング言語ですが,三角関数はあらかじめ用意されています。
ところで,例の塾生の発言。
「サイン・コサインって,いつ使うん?」ですが,実は,続きがあります。
「・・・って,陣〇のネタで言ってた。」
質問ではなく,まさかの報告でした。
ただ,いずれ本当に「いつ使うん?」と思う日が来るかもしれません。
そこで,お休み中にグラフを作成してみました。
こんな感じで(?),第3ターム開講に向けての準備は万端です。
■KEC高槻本校の合格体験談・総集編はこちら
■KEC高槻本校の公式サイトはこちら
/*Scratchでコードを書いてみたシリーズ*/
1 楕円の焦点
2 放物線の焦点
3 ドップラー効果
4 光の屈折
5 転がる円の軌跡
6 動点P
7 曲技飛行
8 さいころの目が一致


