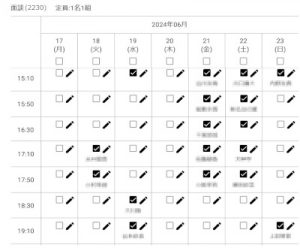
こんにちは。KEC茨木本校2230です。
KECの授業は講師と生徒が対面で行います。
その瞬間に理解してくれているか,確認しながら授業は進みます。
数学の指導では,黒板に張り付いてギャースカしゃべるだけでなく,ちょこっとうろついて皆さんの手元を見に行きます。
何を見たいか?と。
次の3つです。
・よい姿勢で取り組めているか
・使えるノートになっているか
・思考過程が記録できているか
1つめ「よい姿勢で取り組めているか」について。
どこに何を書いているのかがわからないのはいただけません。
イコール記号は1行に1個限定使用,は見やすさ優先のためです。
中ボスレベルの問題をノートの下5行あたりから書き出すと,すぐに次頁に続くことに。頁をめくる作業はミスを誘発します。
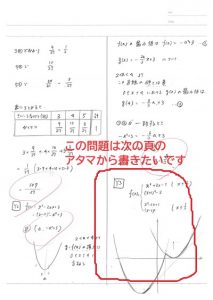
2つめ「使えるノートになっているか」について。
ノートはその時に書いて終わり,ではもったいない。復習で使えるお宝です。
自分がどんなミスをしたのか,赤ペンでメモっておきたいです。解法のツボも書き込むスペースありますか。
また,教材何頁の何番かとか,見出しはつけておきたいです。
3つめ「思考過程が記録できているか」
答案って,上から読ませて,論理が正しければいいわけです。
で,100%イケてる答案を書けてくれることは,今の時点ではあまり期待していません。
むしろ,これから成果につながるための要素を吸収していくことが今のお仕事です。
問題ごとの大方針は?解く過程にどんなポイントがあって,どう考えていくのか。計算作業でのテクは?
こういった,答案が出来上がるまでの影の部分=授業,です。答案完成品を見ても痕跡は見当たらないかも。過程を聞き込みメモっておくことが大切です。ライブ授業の良さってこれじゃないでしょうか。
イケてるノート術で学力アップしてくれたら嬉しいです。