こんにちは。KECの塾・予備校部門,高槻本校の数学・理科担当の川渕です。
KECで11月といえば,能力診断テストの実施月。
通称「のうしん」とよばれる塾生の皆さんの実力テストで,偏差値も出します。
その偏差値,どうやって求めるのでしょうか。
今回は,偏差値の求め方を紹介します。
テストの点数の偏差値を求める式は,以下の通りです。
なんだかややこしそうな式ですね。
高槻本校の高1数学では最近学習したのですが,小中学生の皆さんには,なじみのない用語が出てきました。
高校の数学Iで習う「標準偏差」。
これは,データが平均値からどれくらい散らばっているかを表す指標です。
なぜ,偏差値を計算するのでしょうか。
実際に計算して見ていきましょう。
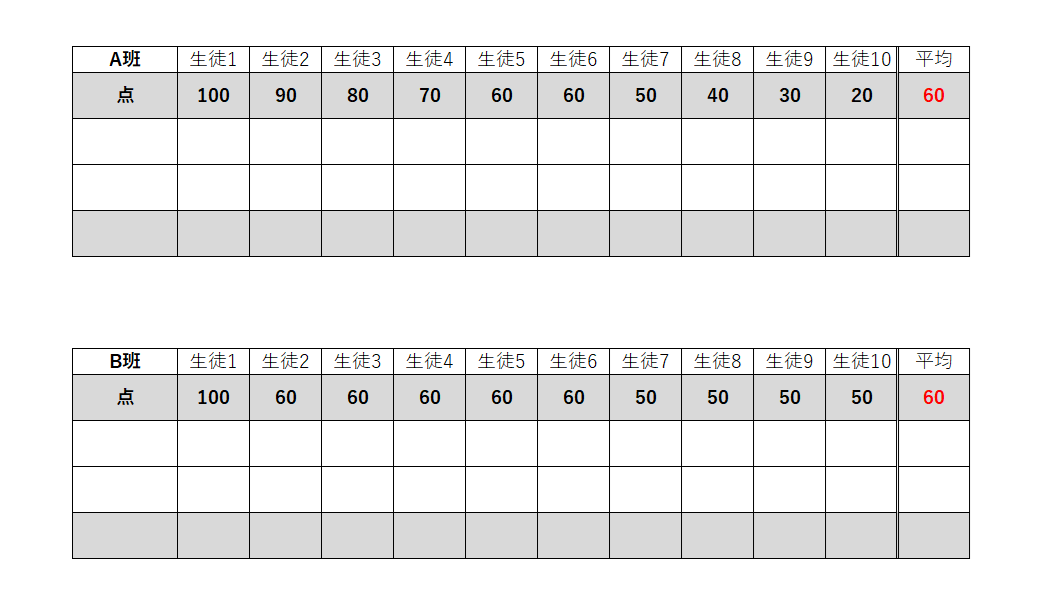
例えば,A班とB班(各10人)で小テストを実施したら,点数がこうなりました。
どちらも平均は60点で同じですが,なんだか,点数の散らばり方が異なります。
B班では,ほとんどの生徒が平均点付近の点数を取っていますね。
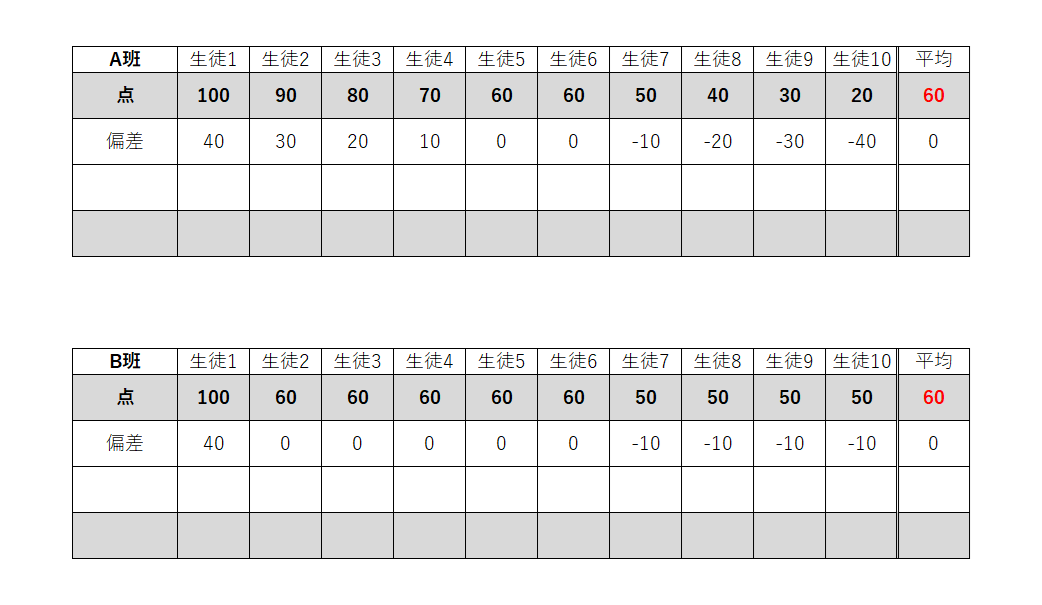
そこで,各生徒が平均点からどれくらい離れているか(偏差)を調べてみます。
偏差を見ると,やっぱり,B班の点数の方が平均点近くに集まっているようです。
そこで,1人1人のばらつきではなく,班全体の散らばり具合をみてみよう・・・と,平均を計算すると,ちょっと困ったことが起こります。
偏差は平均との差なので,和は必ず0になります。
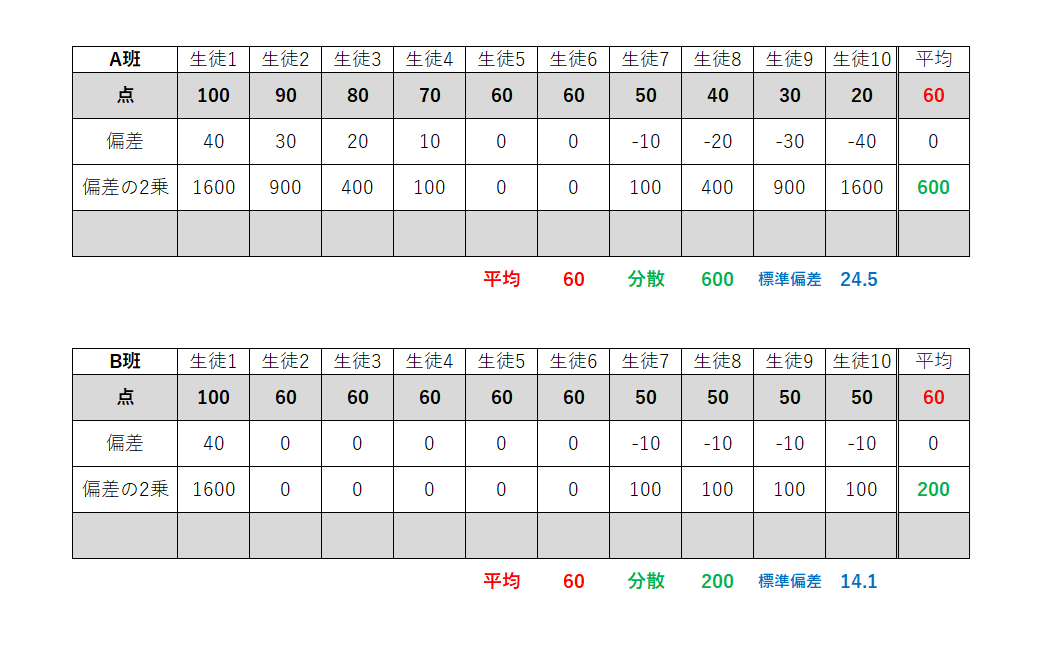
そこで,偏差を2乗してから平均を計算します。
その値を「分散」といいます。
分散を計算すると,平均点からの散らばり具合がわかります。
散らばり具合が大きいと,分散の値も大きくなります。
A班が600でB班が200なので,A班の方が,平均点から散らばっていることがわかりました。
これでデータの散らばり具合はわかりましたが,計算の際に2乗しているので,分散の単位が(点)2になっています。
そこで,分散の正の平方根を計算したものが,標準偏差です。
A班は√600≒24.5,B班は√200≒14.1になります。
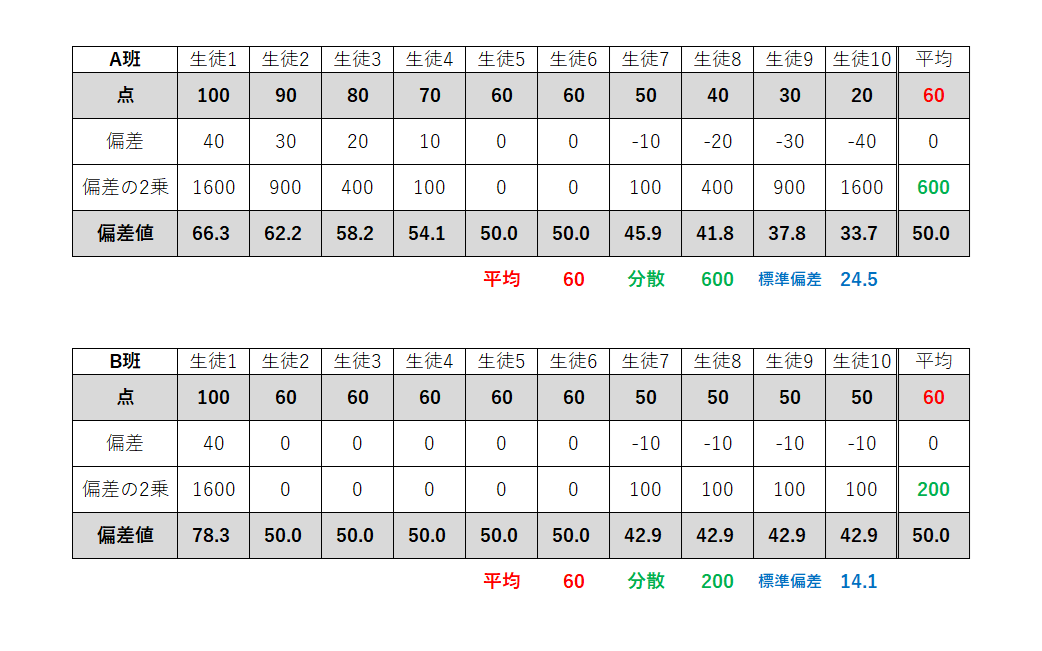
この標準偏差を上の式に当てはめ偏差値を計算すると,以下のようになりました。
上の式にあるように,偏差値を求める計算では標準偏差が分母にあるので,データが散らばっていない(標準偏差が小さい)ほど,偏差値の変化は大きくなります。
例えば,A班とB班のどちらにも100点の生徒がいますが,A班は66.3,B班は78.3と,B班の生徒の方が偏差値が高くなっています。
これは,B班の100点の生徒は,他の生徒が60点,50点のなかで1人だけ100点を取っているので,他の生徒に比べ傑出していそう・・・ということを表しています。
こんな感じで,偏差値を計算すると,集団の中での位置づけを表すことができます。
ということで,KECの実力テスト「能力診断テスト」でも,偏差値を出しています。
KECの能力診断テストは公開テストで,一般生の方も無料で受験可能です。
※一般生の方向けには「志望校判定模試」として実施しています。
高槻本校では,小学生・高校1年生・高校2年生のテストを,11月9日(日)に実施します。
中学生の方は一斉受験は終了していますが後日受験可能です。
次のサイトからお申し込みください。
高校生・中学生・小学生
ぜひ,この機会に自分の学力を確認してみましょう!
*********************************
■合格体験談・総集編はこちら
■KEC高槻本校公式サイトはこちら
■各種イベントのお申し込みはこちら
■アシスタントブログの総集編はこちら
■動画をふくむブログの総集編はこちら
■プリントをふくむブログの総集編はこちら