こんにちは。KECの塾・予備校部門,数学・理科担当の川渕です。
先日,テレビのバラエティ番組をみていたときのこと。
「芸人10人が交代で1曲歌う」という企画をやっていました。
この企画のポイントは,歌う順番が決まっていないこと。
1曲を10のパートに分けているのですが,それぞれ自分の判断で歌い始めるため,歌うパートが被ってしまうことがあります。
「歌う人が被ったらアウト」というルールで,10人が誰とも被らずに歌えるまで,繰り返しチャレンジするというものでした。
さすがに誰とも被らないというのは難しく,芸人の皆さんは苦労している様子。
番組の中で「10人が被らずに歌える確率は,計算上,約1/2756」と紹介されていました。
確率を出されると数学の講師としては気になるところなので,計算してみました。
10人が歌う代わりに,「10人が1から10の間の好きな整数を一斉にいう」と場合を考えます。
彼らがいった整数が,歌う順番を表すとします。
ということで,この問題を「10人が1から10の間の整数を一斉に答えるとき,その数字が被らない確率を求める」として計算します。
まず,すべての答え方が何通りあるかを求めます。
10人がそれぞれ10通りの答えを言うので,すべての答え方は1010(10の10乗)通り。
次に,被らない答え方が何通りあるかを求めます。
答えが被らないときは,10人の答えが1から10のいずれかになっているはずなので,被らない答え方の総数は1から10の並べ方の総数に等しく,10!(10の階乗)通り。
よって,求めたい確率は,
(被らない答え方の総数)/(答え方の総数)
=(10!)÷(1010)
=567/1,562,500
となり,番組内で紹介された確率とあいません。
ただ,分子を1にすると
約1/2755.73…
となるので,ほぼ,1/2756に等しくなりました。
ついでに,Excelでシミュレーションもしてみました。
AからJの10人分の乱数を3000回発生させて,10人の答える数字が被るかどうか調べました。
何回か調べたのですが,例えば,この時は451回目に被りませんでした。
RANDBETWEEN(1,10)で1から10の乱数を発生させます。
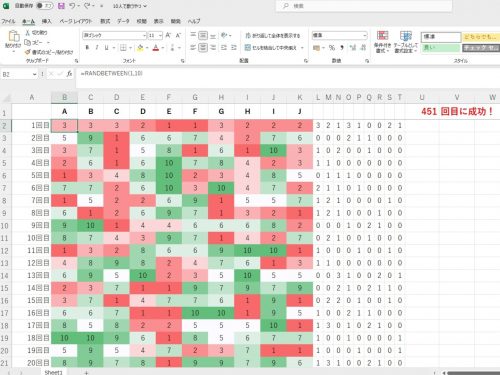
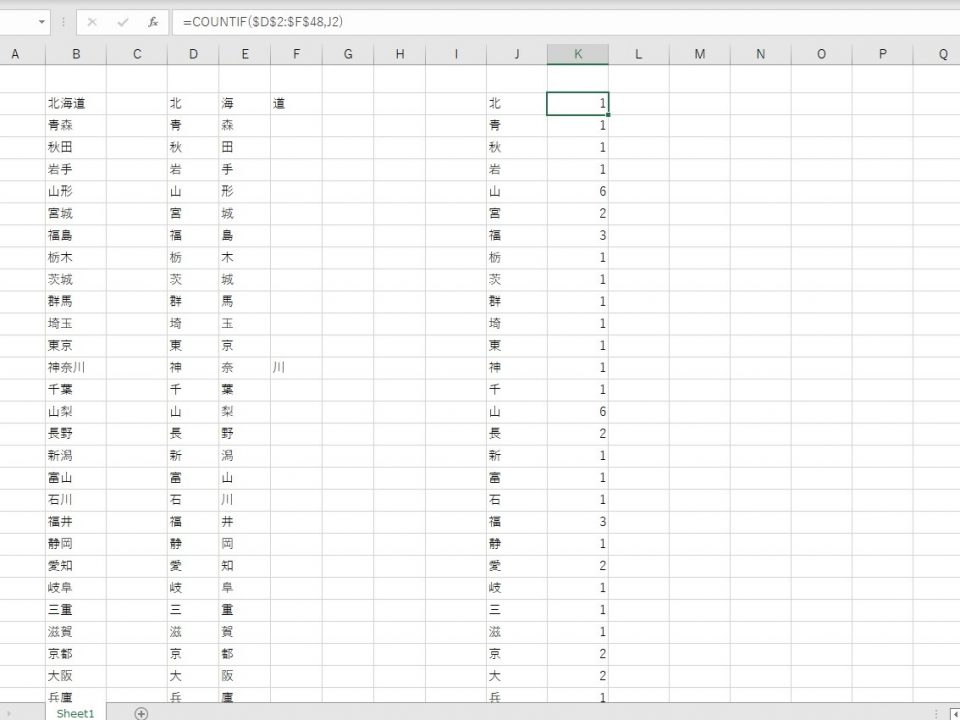
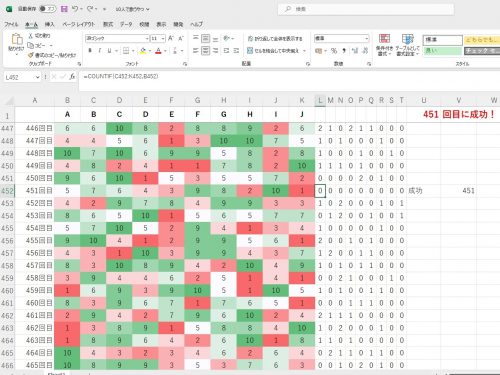
A~Jの数字が被るかどうか,自分より右の数をすべて調べて被る回数をカウントしています。
被る数が無ければ右のL列からT列の9個の数字はすべて0になります。
※ここでは,L列からT列の和が0になれば「成功」と表示されるようにしています。
番組のように実際に歌って一致するかどうか調べるとなると,本当に大変そうですね。
こんな感じで,小ネタの用意に余念がない高槻本校では,小学生・中学生・高校生の無料体験授業を実施中。
1クラス平均10人前後の,小人数クラスで体験もしやすいです。
ぜひ,この機会にKEC高槻本校までお問い合わせください。
*********************************
■合格体験談・総集編はこちら
■KEC高槻本校公式サイトはこちら
■各種イベントのお申し込みはこちら
■動画をふくむブログの総集編はこちら
■プリントをふくむブログの総集編はこちら