こんにちは。KECの塾・予備校部門,高槻本校の数学理科担当の川渕です。
2026年の大学入学共通テストが終わりました。
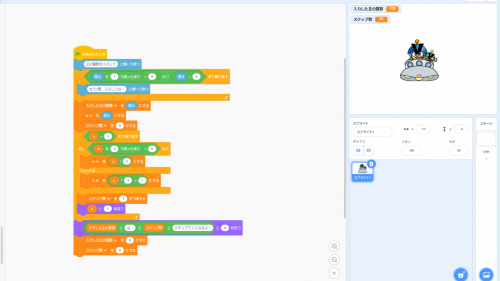
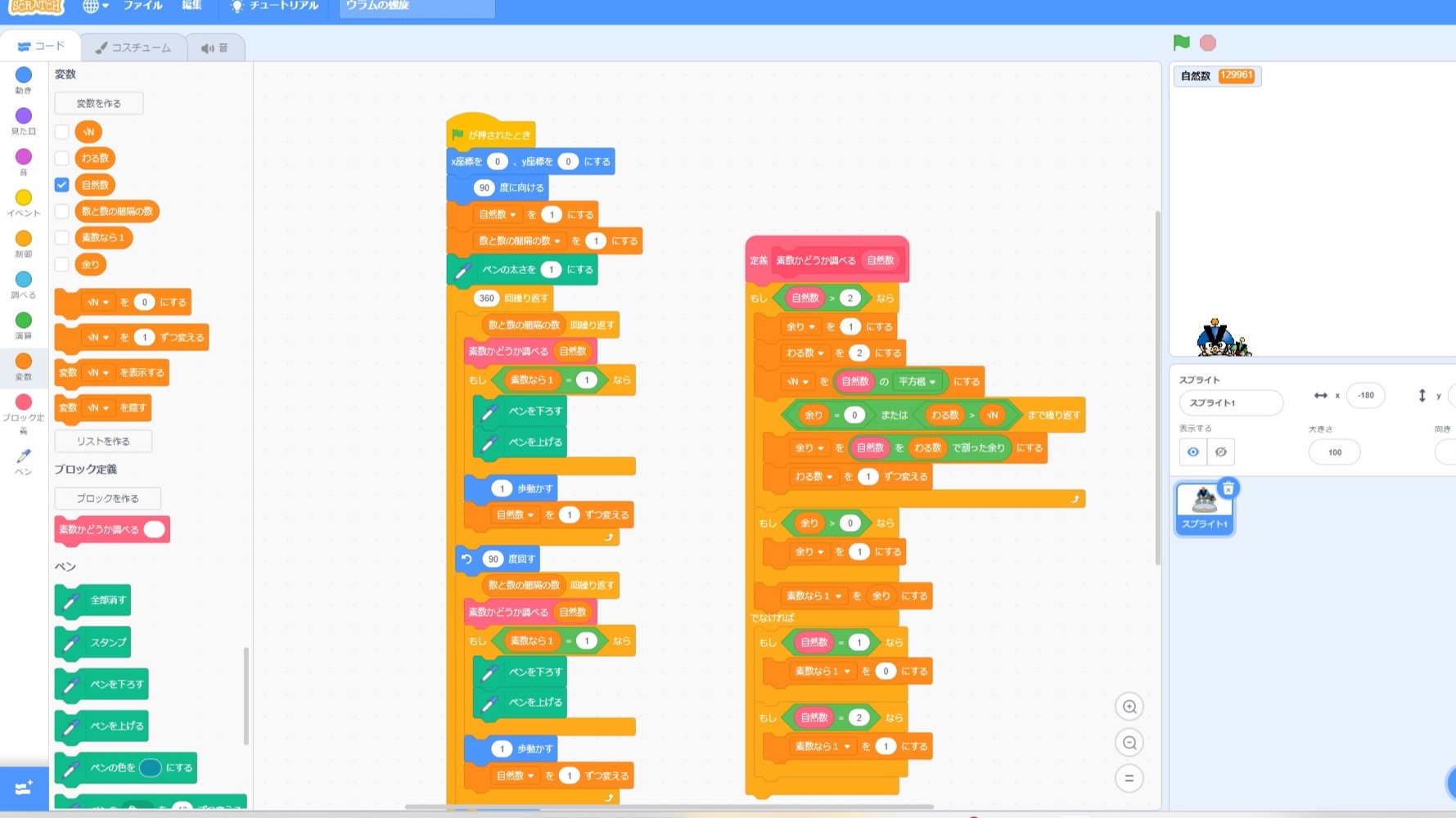
昨年から始まった「情報I」,第3問にプログラミングの問題が出題されますが,昨年に引き続き,今年もScratchで再現してみました。
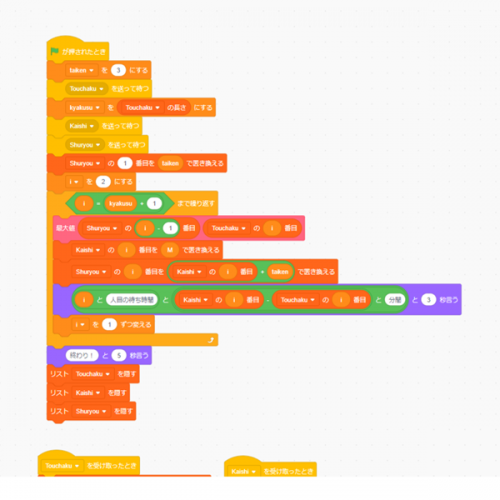
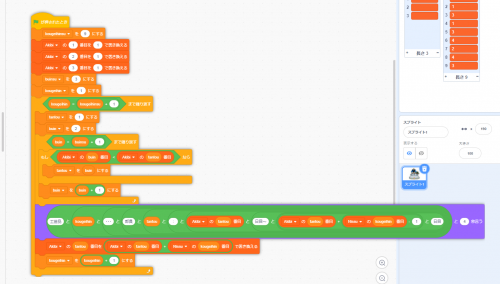
まず,問2の待ち時間を計算するプログラム。
文化祭でゲーム体験に来た人が,1人3分ずつ体験するとして待ち時間が何分になるかを計算します。
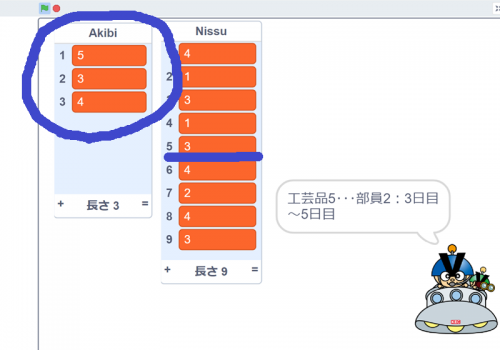
「Touchaku」というリスト(配列)には,来訪者(6人)の到着時刻が入ります。
「Kaishi」と「Shuryou」には,各来訪者の開始時刻,終了時刻が入ります。
仕様が異なるので,問題そのままとはいきませんでしたが,こんな感じにしました。
配列を初期化したり,最大値を求めたりするのは,関数などにしてみました。
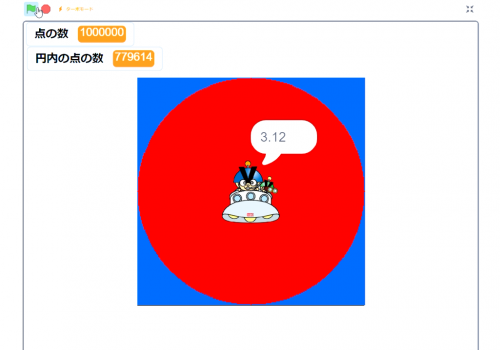
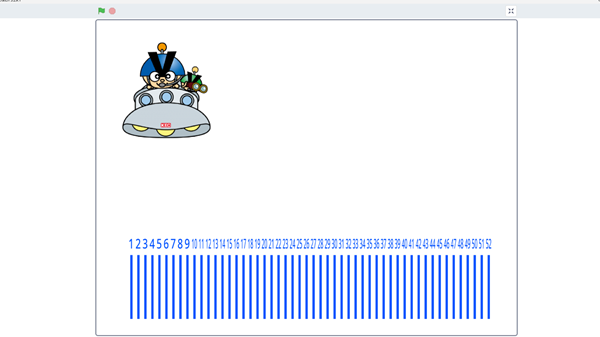
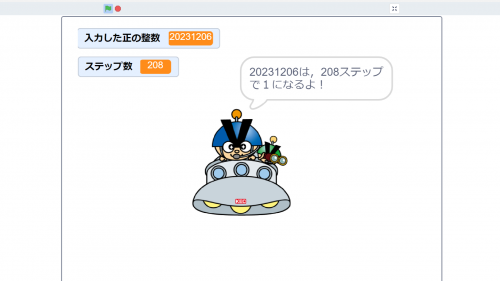
実行すると,謎のUFOが待ち時間を読み上げてくれます。
次は,問3の最長待ち時間を計算するプログラム。
体験時間を変更(1分~15分)すると,最長待ち時間がどう変わるかを調べます(最長待ち時間が10分を超えると表示しない)。
あとの問題で出てくるので,配列Kaishiの初期化処理の実行回数もカウントしてみました。
実行すると,たしかに15回処理をしていますが,後半は最長待ち時間が10分を超えているので,計算を省いてもよさそうなことがわかります。
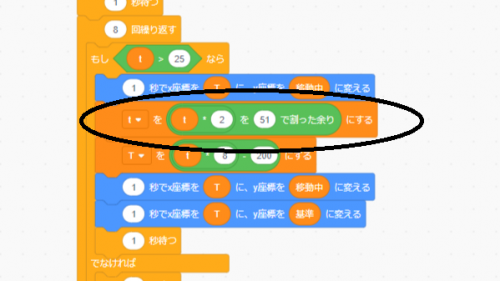
最後に,第3問の後半,最長待ち時間が10分以上になったら止まるプログラム。
問題文にある繰り返しの条件「(taiken <= 15) and (saichou < 10)の間繰り返す:」をScratchでどうすればよいかわからなかったので,「 (taiken > 15)or (saichou > 9)まで繰り返す:」に変えました。
実行すると,確かに初期化が5回で止まりました。
問題に出てくるプログラムを再現すると,とても勉強になりますね!
こんな感じで,入試問題の研究に余念がない(?)KEC高槻本校では,塾・予備校をお探しの方向けに,体験授業をお勧めしています。
特に,2月から,現高2生向けには「リスタート講座」,現小6生向けには「新中1スタートダッシュ講座」を開講します。
もちろん,現高1生や,中2生,中1生,小5生,小4生の体験も大歓迎です。
・・・上の段落の文章は,ほぼ昨年のブログの再現なのですが,毎年,この時期に多くの方にKECをお選びいただいています。
ぜひ,この機会にKEC高槻本校の授業を体験してみてください!
*********************************
■合格体験談・総集編はこちら
■KEC高槻本校公式サイトはこちら
■各種イベントのお申し込みはこちら
■アシスタントブログの総集編はこちら
■動画をふくむブログの総集編はこちら
■プリントをふくむブログの総集編はこちら