みなさん、こんにちは。KEC塾予備校 楠葉(くずは)本校の松田です。
先日、ある塾生から「先生って、KECで何年働いているの?」と聞かれました。「15年やで。」と言うと、「え?私が生まれる前から??」と驚かれました。
KEC楠葉本校も15年なんだけどね…( ̄▽ ̄)
前も一度書きましたが、授業のこだわりです。
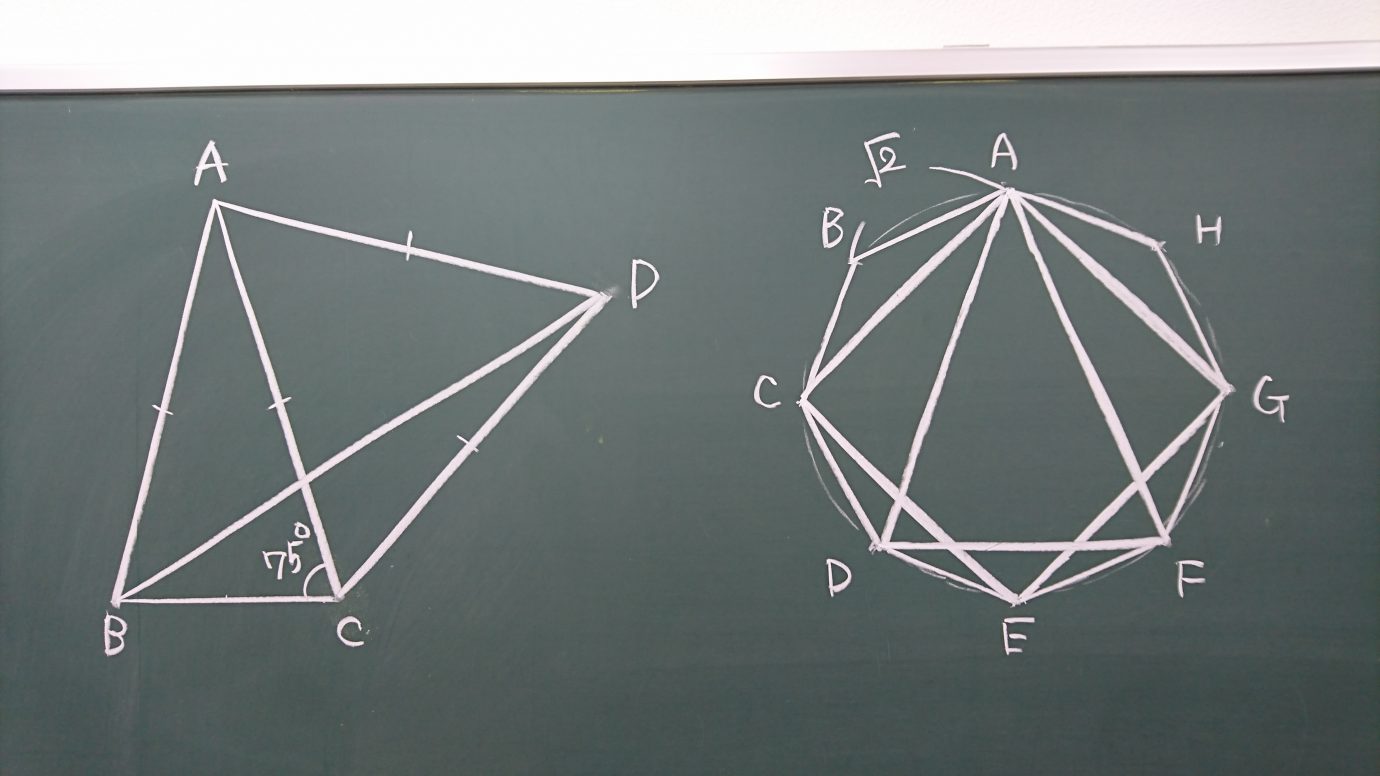
私が塾の先生の駆け出しのころに教えられたのは「数学の先生の黒板にかく図形が不正確だと、子どもたちはわからんよ!」です。今も大切にしているその一言で、何回も何回も黒板に図形をかく練習をしました。
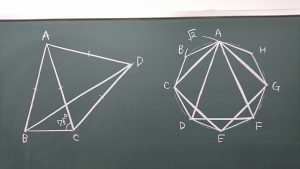
板書してみました!
この間、他の先生から「図、めちゃ上手ですね。」
私としては当然のことなのですが、褒められると嬉しいものです^^
以前載せたネタではありますが、黒板の図形に関する技術的なお話を載せておきますね。
《正八面体の作図》
正八面体とはこんな図形です。ちょっとしたアイデアで、フリーハンドで結構うまく書けるんですよ。

では、ネタばらし!まずはひし形または平行四辺形をかきます。もちろん、線をまっすぐに引くこと、線を平行に引くことは練習あるのみ!

次に、こんな感じで線を入れて….

仕上げに点線をかくと、できあがり!

興味がある人は、やってみてくださいね~♪

KEC近畿予備校・KEC近畿教育学院 楠葉本校 ← click here
072-850-8888