こんにちは。KEC茨木本校2230です。
皆さんの合格を願って励む2230ほかスタッフ一同ですが,時には神様仏様縁起物にもすがります。
共通テスト受験日に勝尾寺へ走るのは定番となっておりますが,今秋はマンホール趣味に目覚めました。マンホールふたはその丸い形から,どんな角度でも穴に「落ちない」,表面に凹凸があり「滑りにくい」ことから受験生にとって縁起が良いものです。
高槻市と企業のコラボマンホールの件は以前のブログでお知らせしましたとおりですが,今回はその後の追加ネタです。あちこち走ってGETしてきました。
高槻の上宮天満宮は,学問の神様・菅原道真を祀る,大宰府に次いで2番目に古い天満宮だそうで,受験生やそのご家族に親しまれるとともに崇敬を集めております。
地元企業とのコラボで,合格祈願マンホールふたを制作,11月に奉納式が行われたそうです。

このキャラはサンユレくんといいまして,菅原道真をオマージュしたコラボ企業先のキャラだそうです。上宮天満宮の本殿を組み合わせたデザインは,かわいくご利益がありそうですね。
国土交通省からもグッズプレゼントがありましたので飛びつきました。
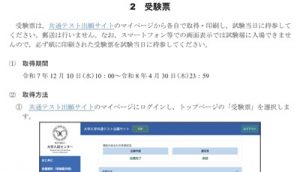
合格祈願カード付きマンホールカードセットが500セット限定。

もずやんですね,缶バッチ付きです。
東大阪の鴻池水みらいセンターにて朝9時配布開始にあわせ,7時半に家を出ました,一番乗りでした。
近隣でのマンホール情報をお待ちしております。