こんにちは。KECの塾・予備校部門,高槻本校の数学・理科担当の川渕です。
高槻市内の公立高校では,一部を除いてテスト期間に入りました。
高1の塾生が勉強していたプリントをみると,物理基礎の速度の合成の問題でした。
速度の合成といえば,対岸に渡ろうとする船が流水に流されたりする問題です。
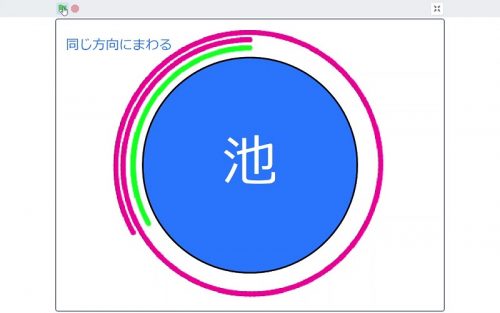
そこで,久しぶりにScratchでコードを書いて,UFOが川に流されるようす(?)を再現してみました。
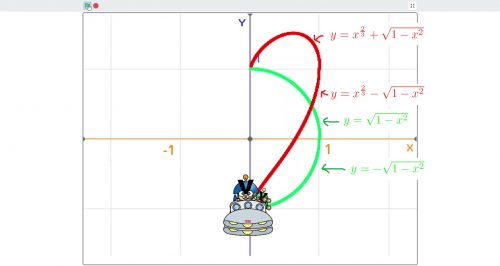
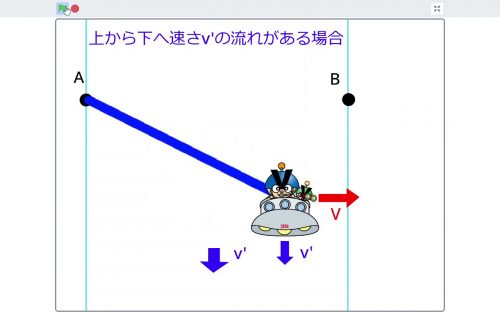
A地点から対岸のB地点へ,恒例のUFOが渡ろうとしています。
静水時の船の速度と川の流れが垂直な場合は,対岸の到着時間に差がありません。
v’と合成した分,船自体の速度は速くなりますが,速度の流れに垂直な成分(動画でいうとV)の大きさが変わらないからです。
そのため,対岸に到着するのにかかる時間はVで計算できます。
B地点から流されたB‘地点までの距離は,v’で求めます。
こうして動画を作ってみたのですが,なんだか,UFOの動きが人生のように見えてきました。
今はテストで大変ですが,なにかと楽しいことが多い高校生活。
いろいろ流されることはありますが,3年で卒業するのは,みな同じです。
目標地点と離れた位置に到着しないよう,しっかりと針路を取って過ごしましょう!
Scratch 3.22.0
■合格体験談・総集編はこちら
■KEC高槻本校公式サイトはこちら