こんにちは。KECの塾・予備校部門,高槻本校の数学・理科担当の川渕です。
先日,中3数学の授業で「円周角の定理の逆」を取り扱いました。
下の図で,「∠APB=∠AQBが成り立つとき,4点A,B,P,Qが同一円周上にある」というもの。
見えない円を探さないといけない,という点で難しい円周角の定理の逆。
探すコツとして「角周円ちゃんを探せ!」と塾生に伝えています。
「円周角」の逆だから,「角周円」と名付けました。
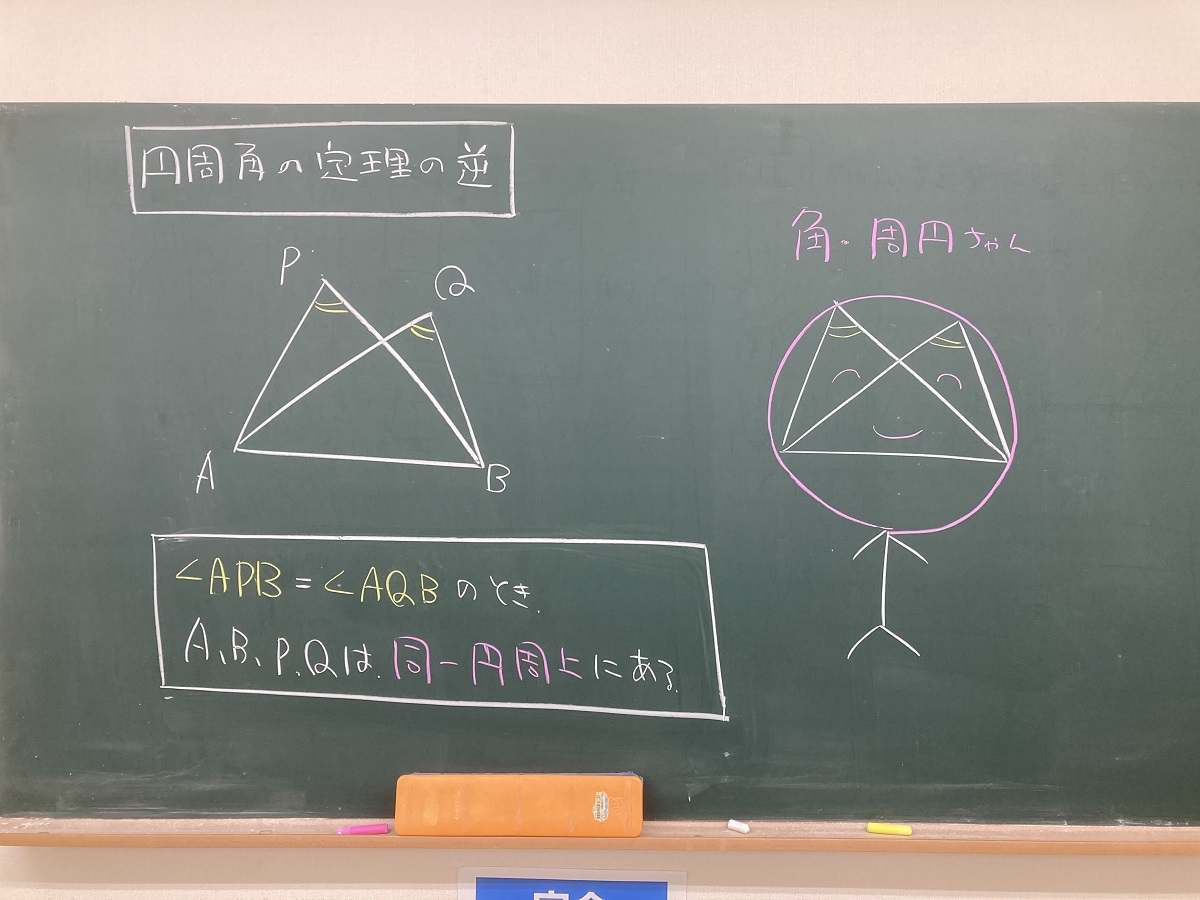
図で分かるように,私の授業では棒人間を多用しています。
ここで,私が学生時代に習った「公開鍵暗号」を棒人間で説明してみましょう。
最近は高校の「情報」の授業で習うようですが,私は大学で習いました。
データを送信するとき,第三者にバレないようにするには暗号が必要です。
送信者と受信者で一つの鍵(共通鍵)を共有して暗号をかければ,安全に送受信できます。
これを「共通鍵暗号方式」といいます。
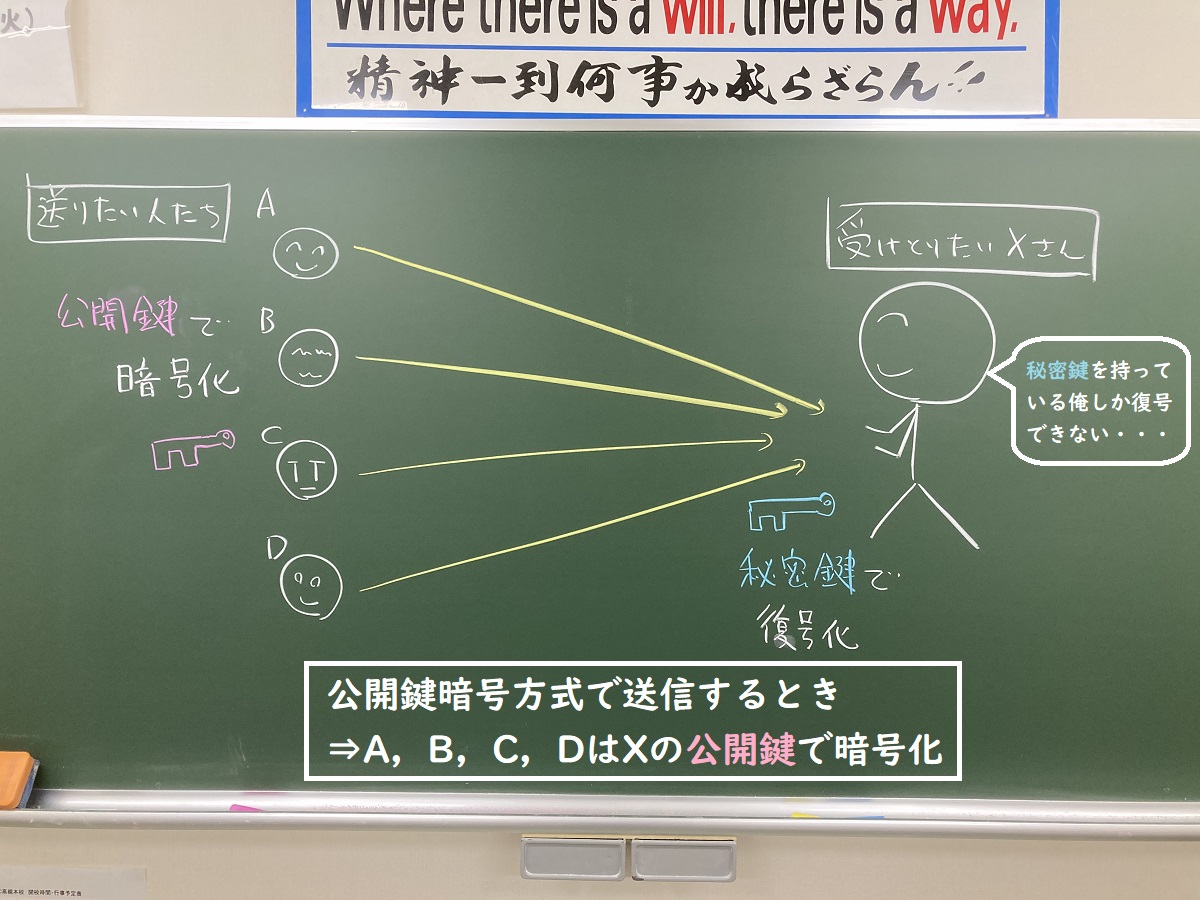
A,B,C,Dの4人がXさんにデータを送信するとき,お互いにデータがバレないようにそれぞれの共通鍵で暗号化します。

それに対し,受信者が「公開鍵」と「秘密鍵」の2つをペアで作成し,公開鍵を送信者に伝えて「この鍵で暗号をかけてね」というのが「公開鍵暗号方式」。
Xさんに何か伝えたいとき,みんなが同じ公開鍵を使ってもお互いにバレることはありません。
その暗号文を復号(元に戻せる)のが,秘密鍵を持っているXさんだけだからです。
多人数で情報をやりとりするときは,公開鍵暗号方式の方が鍵の総数が少なくて済みます。
また,共通鍵暗号方式では相手に共通鍵を安全に送らなければなりませんが,そのために公開鍵暗号を使ったりするそうです。
この公開鍵暗号で使われている数学の理論の1つに,中1で習う「素因数分解」があります。
素因数分解をもとにして作った暗号を,RSA暗号というそうです。
ざっくりいうと「答えがわかっている人には簡単に確かめられるけど,そうでない人には解くのが難しい」という性質が暗号にピッタリとのこと。
これを大学で習った私は「こんなことを思いつくなんて,世の中には,賢い人がいるなあ・・・(ちなみに,R・S・Aは,発明者の3人の頭文字だそうです)」と驚いたものですが,この公開鍵暗号,公開鍵で暗号化して秘密鍵で復号化するだけでなく,逆の利用法もあります。
こんな感じです。
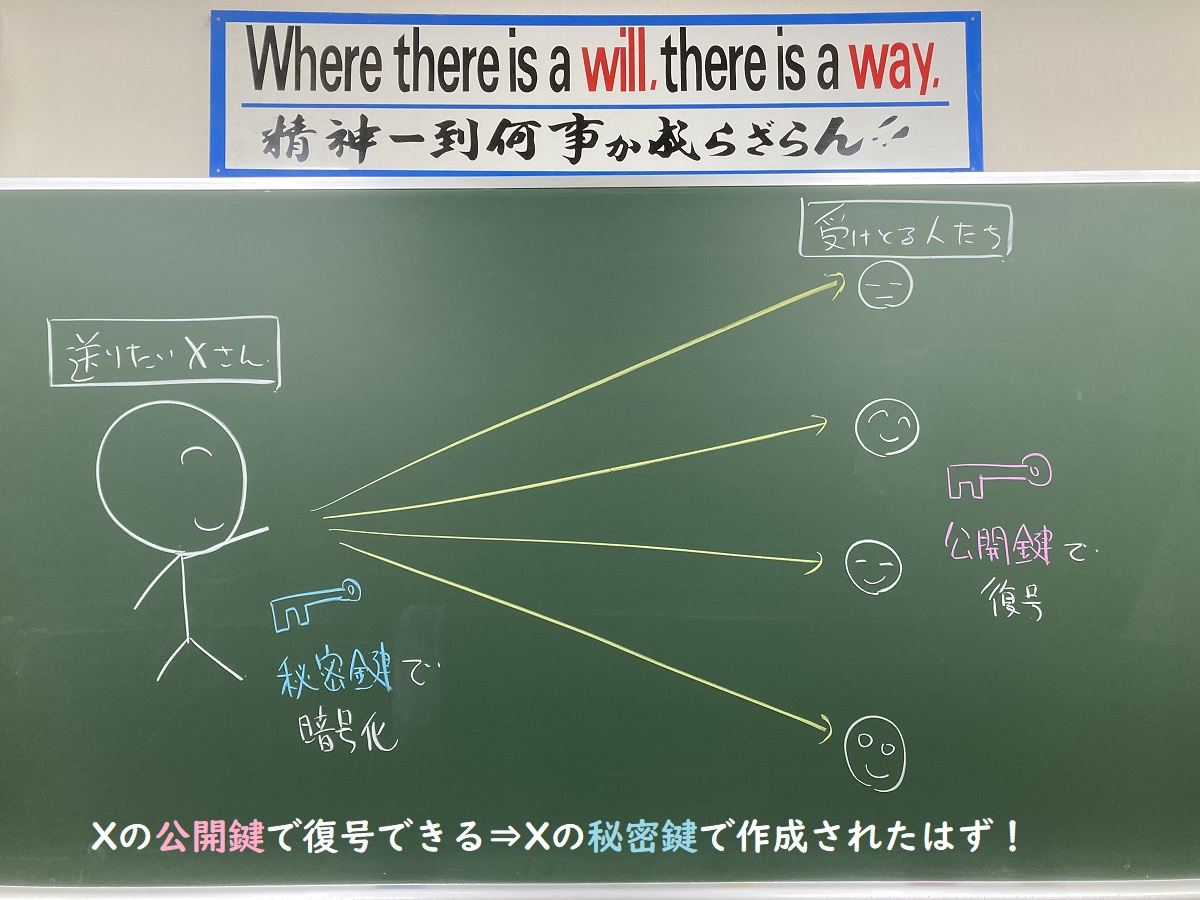
Xさんがデータを処理してから,自分の秘密鍵で暗号化した処理済みデータと暗号化する前の処理済みデータを送信し,「これを公開鍵で復号してね」と伝えます。
データを受信した人達は「公開鍵で復号したものと暗号化する前のものとが一致するから,これはXさん本人が送ったものに間違いない」と確認ができます。
本人確認のためのサインと同じようなものなので,これを「署名」というそうですが,こんなことを考え出す人って,本当,すごいですね。
※実際には,もっと難しい話があって単純に公開鍵暗号と署名は逆というわけではなく,別の技術なのだそうです。
さて,棒人間が活躍する高槻本校では,小学生・中学生・高校生対象に,授業の無料体験を実施しています。
KEC高槻本校の授業はすべて公開していますので,どの授業でも体験可能です。
ぜひ,この機会にKEC高槻本校の高い合格率の秘密に触れてみてください!
■合格体験談・総集編はこちら
■KEC高槻本校公式サイトはこちら